Formal Semantics

Details of the formal semantics of POOSL can be found in:

L.J. van Bokhoven, Constructive tool design for formal languages: from semantics to executing models, PhD thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2002. DOI

The semantics of the data layer is defined as a probabilistic denotational semantics. It generally follow the behaviour of traditional object-oriented languages like Java. Its probabilistic nature is derived from an explicit modeling of probabilistic behaviour introduced by RandomGenerator objects.

The semantics of the process and architecture layers is defined as a probabilistic, timed, structural operational semantics similar to process calculi such as CCS or CSP. The probabilistic behaviour of processes originates from the probabilistic behaviour of data objects. The semantics of POOSL follows a two-phase execution model. The state of a model can either change by asynchronously performing actions or by synchronous passing of time. Time only advances if there are no actions that can be performed immediately (action urgency). The semantics ultimately defines a timed probabilistic labelled transition system of the form

${\cal M} = \left( {\cal C}, C_s,{\cal A}, \left\lbrace \xrightarrow{a} \subseteq {\cal C}\times {\cal D}({\cal C}) \mid a\in {\cal A} \right\rbrace, {\cal T}, \left\lbrace \xrightarrow{t} \subseteq {\cal C}\times {\cal C} \mid t\in {\cal T}^+ \right\rbrace \right)$

It includes a set ${\cal C}$ of configurations, each reflecting a possible state of the model during its execution. The initial configuration $C_s \in {\cal C}$ represents the initial state of the model at the start of its execution. A configuration $({\cal B}, {\cal I})\in {\cal C}$ includes the specification of behaviour ${\cal B}$ that is to be executed in the context of information ${\cal I}$ . Behaviour ${\cal B}$ indicates the statements describing the (future) behaviour of an executing model, while information ${\cal I}$ captures the data objects that are assigned to global and local variables. The timed probabilistic labelled transition system ${\cal M}$ furthermore includes a set ${\cal A}$ of actions, a time domain ${\cal T}$ and two sets of labelled transition relations. For ${\cal A}$ , three kinds of elements are distinguished:

the internal action $\tau$ and fix action $f$ , representing computations that are unobservable by the environment of an executing model;
communication actions of the following two forms. A send action $p!m(v_1,\ldots,v_n)$ denotes sending message $m$ with parameters $v_1,\ldots,v_n$ to port $p$ , whereas the receive action $p?m(v_1,\ldots,v_n)$ indicates receiving message $m$ with parameters $v_1,\ldots,v_n$ from port $p$

The elements of the two sets of labelled transition relations are defined based on the semantical rules and axioms for the statements in table 2. The set $\left\lbrace \xrightarrow{a} \subseteq {\cal C}\times {\cal D}({\cal C}) \mid a\in {\cal A} \right\rbrace$ denotes the action transitions for a model, where ${\cal D}({\cal C})$ is the set of distribution functions over ${\cal D}({\cal C})$ ;

${\cal D}({\cal C})=\left\lbrace \pi: {\cal C} \rightarrow [0,1] ~\middle| ~ {\sum_{C\in{\cal C}} \pi(C)} =1 \right\rbrace$

In configuration $({\cal B},{\cal I})\in{\cal C}$ , relation $({\cal B},{\cal I})\xrightarrow{a}\pi$ holds if action $a\in A$ can be performed, after which the model transits to configuration $({\cal B}', {\cal I}')$ with probability $\pi({\cal B}', {\cal I}')$ , for each $({\cal B}', {\cal I}')\in{\cal C}$ . In case several (different) actions can be performed, the choice of which action is executed is made non-deterministically. Then, a probabilistic choice determines the resulting configuration. In a simulation tool, such as Rotalumis, the non-deterministic choices may be resolved randomly, or by means of user interaction.

The set $\left\lbrace \xrightarrow{t} \subseteq {\cal C}\times {\cal C} \mid t\in {\cal T}^+ \right\rbrace$ denotes the time transitions for a model. In configuration $({\cal B},{\cal I})\in{\cal C}$ , relation $({\cal B},{\cal I})\xrightarrow{t}({\cal B}',{\cal I}')$ holds if the time can pass for $t\in{\cal T}^+$ units of time, where ${\cal T}^+ = \left\lbrace t\in{\cal T} \mid t>0 \right\rbrace$ . A model only has time transitions for the maximal amount of time that it is willing to wait before continuing with performing action transitions, where it is implicitly understood that it is also willing to wait for a shorter time. As a result, there is at most one $t$ and $({\cal B}', {\cal I}')$ for each $({\cal B}, {\cal I})\in {\cal C}$ such that $({\cal B}, {\cal I})\xrightarrow{t}({\cal B}', {\cal I}')$ holds. Hence, time transitions are deterministic (taken with probability 1).

Transition system $M$ can be visualised as a graph. The nodes of this graph represent the configurations of $M$ . The initial configuration $C_s$ is identified with a symbol > directed towards the node. For any action transition relation $C\xrightarrow{a}\pi$ with $\pi\in {\cal D}({\cal }c)$ , a directed double (multi) arrow is drawn from node $C$ to all nodes $C'$ to which the system can transit with positive probability $\pi(C')$ . The first part of the double (multi) arrow is a directed arrow labelled with action $a$ and the second part is a fan-out of directed arrows labelled with the probabilities $\pi(C')$ . For any time transition relation $C\xrightarrow{t}C'$ , a directed arrow is drawn from node $C$ to node $C'$ , which is labelled with $t$ . Since time transitions denote the maximal amount of time that the model is willing to wait before continuing performing action transitions, $t$ is either a (positive) number or $\infty$ . The following example illustrates visualisation of the transition system corresponding to the behaviour specified by one process method.

Example

Generating bursts of (fixed-size) packets can be specified with the process method GenerateTraffic in figure 2. In line 1, a local variable p of type Packet is declared. The actual behaviour specification of GenerateTraffic starts in line 2 with the creation of a new instance of data class Packet. After creating the new packet, its identifier is set to PacketNumber. In line 3, PacketNumber is incremented to ensure that the identifier of the generated packet is unique. The braces in lines 2 and 3 specify that the enclosed expressions are to be executed as one indivisible action. The send statement in line 4 specifies sending p through port Out. The duration of sending p, which equals the size PacketSize of a packet divided by the (fixed) rate Bandwidth with which packets are sent, is modelled with the delay statement in line 5. Line 6 models the probability of inserting a period without traffic after sending p. To this end, a sample is drawn from the Bernoulli distribution InsertIdleTime. If sending another packet must be postponed, the delay statement in line 7 is executed. The exact time to wait depends on a sample drawn from the discrete uniform distribution IdleTimeDistribution. Infinite repetition of sending a packet and inserting an idle period is modelled with tail-recursion in line 9.

  GenerateTraffic()() |p: Packet|
    {p := new(Packet) withNumber(PacketNumber);
    PacketNumber := PacketNumber + 1};
    Out!Packet(p);
    delay(PacketSize / Bandwidth);
    if InsertIdleTime yieldsSucces then
        delay(IdleTimeDistribution sample)
    fi;
    GenerateTraffic()().

Figure 2. Generating bursts of packets.

When abstracting from the actual values of p and PacketNumber, the timed probabilistic labelled transition system defined by method GenerateTraffic can be visualised as shown in figure 3. The initial configuration C1 reflects the behaviour specified by the expressions of lines 2 and 3. The internal action transition from C1 to C2 originates from creating a new packet and incrementing PacketNumber in lines 2 and 3 together (because of the braces) and is performed with probability 1. The send statement in line 4 specifies the send action transition from configuration C2 to C3. Remark that send action Out!Packet denotes a synchronisation with the environment. If the environment is not prepared to participate in performing a matching receive action, execution of Out!Packet is postponed until the environment is ready to receive the packet. Hence, the send statement also specifies the time transition from C2 to C2 labelled with , which denotes the willingness to wait for an arbitrary amount of time before performing send action Out!Packet.

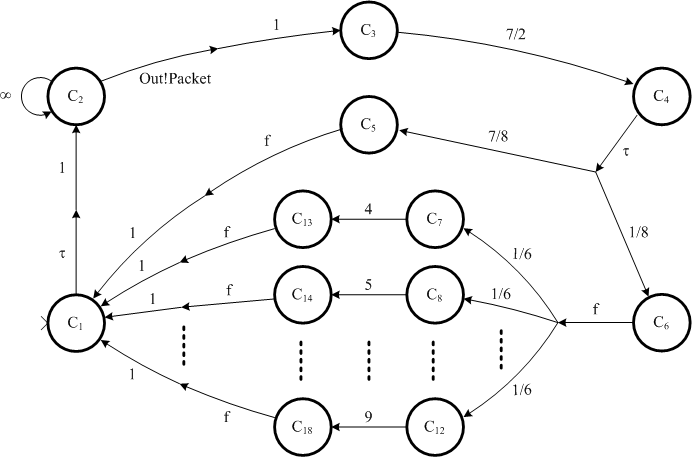
Visualisation of a timed probabilistic labelled transition system

Figure 3. Visualisation of a timed probabilistic labelled transition system.

The time transition from configuration C3 to C4 originates from the delay statement in line 5 of figure 2. The label 7/2 is obtained by assuming that PacketSize equals 140 data units and the rate Bandwidth of sending packets is 40 data units per time unit. The if statement in line 6 results in an internal action with branches to configurations C5 and C6. Assuming that the Bernoulli distribution InsertIdleTime yields success with probability 1/8, the system transits to C5 if no idle period has to be inserted and to C6 otherwise. From configuration C5, the fix action transition to C1 reflects the tail-recursive call of method GenerateTraffic. On the other hand, the part of the transition system in figure 3 regarding configurations C6 to C18 is the result of the delay statement in line 7. This delay statement illustrates how probabilistic timing behaviour can be specified in POOSL. Its execution first involves evaluating the amount of time to wait. Suppose that IdleTimeDistribution is a discrete uniform distribution assuming the values 4, 5, 6, 7, 8 and 9. Then, the resulting fix action has branches to 6 different configurations, which are all entered with the same probability. From these configurations, the time can pass for an amount equal to the involved sample of IdleTimeDistribution and after that the system resides in the corresponding configuration C13 to C18. Finally, the fix actions from these configurations to C1 reflect the tail-recursive call of method GenerateTraffic.